고대 그리스의 수학에도 무한 개념은 존재하였다. 다만 그 개념이 명확하게 정의되지 않은 상태였다. 제논은 역설을 통하여 당시 사람들이 생각하는 무한 개념의 모순점을 지적하였다.
그 당시엔 제논이 제시한 역설을 반박하기가 매우 어려웠으며, 이런 역설로 인하여 사회를 어지럽힌다.라는 이유로 왕에게 미움을 받아 처형당했다.
하지만 제논의 역설은 오랜 기간 동안 해결하기 위해 많이 논의되어왔고 수학의 발전에 많은 영향을 끼쳤다.
19세기 초 코시(Augustin Louis Cauchy, 1789~1857)가 무한급수의 특성, 연속, 극한에 대하여 명확하게 규정하고, 19세기말 게오르크 칸토어(Georg Cantor, 1845~1918)의 무한집합론이 나오면서 직선 위의 실수는 자연수처럼 하나씩 셀 수 있는 무한대보다 훨씬 더 많다는 것을 증명해 보이면서 이러한 제논의 역설의 모순을 찾아낼 수 있었다.
칸토어는 집합론의 창시자로 실수의 개념을 엄밀하게 정의하고 대각선 논법을 통하여 자연수와 유리수는 일대일대응이 되어 그 개수(농도)가 같은 무한집합이지만 실수는 자연수보다 그 개수(농도)가 훨씬 더 많다는 것을 증명함. 독일에서 레오폴트 크로네커에게 수학을 배우고 자신이 연구한 무한집합론을 비판받을 것을 걱정하여 십여 년간 발표를 미루다가 발표를 하였으나 예상대로 레오폴트 크로네커, 앙리 푸앵카레 등 많은 유한주의와 직관주의 수학자들의 비판으로 우울증과 정신질환으로 정신병원에서 사망하였다.
자연수나 유리수의 집합은 셀 수 있는 가산집합(countable set)이고, 실수나 복소수는 셀 수 없는 비가산집합(uncountable set)이다. 즉, 시간처럼 셀 수 없는 연속성을 갖는 무한대를 어느 한순간을 경계로 하여 쪼개는 것은 불가능한 것이다.
자연수의 집합은 무한집합이다. 그렇지만 셀 수 있는 무한집합이다.
인류는 오랫동안 하나도 빠짐없이 셀 수 있는 방법을 찾고자 노력해왔고 마침내 일대일대응이라는 방법을 찾아내었다. 큰 새장 속에 수많은 새가 섞여 있을 때 새들을 하나도 빠짐없이 센다는 것은 어려운 일이다. 그러나 모든 새 다리에 리본을 묶으면 새들이 섞일지라도 묶은 리본의 수를 통하여 새가 몇 마리인지 알 수 있다. 새 전체를 A라는 집합으로 볼 때 새의 숫자를 집합 A의 기수(cardinal number)라고 한다. 새 전체의 집합 A와 새 다리에 묶은 리본의 집합 B는 같은 기수를 갖는다.
유한집합 또는 무한집합이든 관계없이 두 집합이 일대일대응이면 같은 기수를 갖는다. 무한은 특정한 큰 수를 나타내는 것이 아니다. 큰 수로는 불교에서 유래한 항하사(갠지스 강의 모래의 수로 10^56(10의 56 제곱)을 의미함), 무량대수(10^88)가 있는데 숫자로의 기능보다는 철학적인 의미를 내포하고 있다고 봐야 한다. 구골(Googol)은 10^100을 나타내는 숫자로 인터넷 검색엔진 업체 구글(Google)은 처음에 구골(Googol)로 등록하려다가 실수로 잘못 표기하여 지금까지 쓰이고 있다고 한다.
무한은 보통 무한대로 불리며 숫자가 아닌 무한히 커지는 상태로 로 표기한다. 이상적인 개념으로 극한이라는 의미를 포함하고 있다.
무한대에 아무리 큰 수를 더하거나 곱하여도 무한대보다 크다고 말할 수 없다.
갈릴레이 갈릴레오는(Galileo Galilei, 1564~1642)는 자연수의 집합 A={1, 2, 3, 4···}, 자연수 제곱의 집합 B={1, 4, 9, 16···} 에서 집합 B는 자연수 집합의 일부이므로 집합 A의 진부분집합이다. 유클리드 공리에 따라서 전체는 부분보다 크므로 집합 B의 원소의 개수는 집합 A의 원소의 개수보다 적어야 한다고 하였다.
그런데, 집합 B의 원소의 개수는 집합 B의 원소의 양의 제곱근의 개수와 같고 이는 자연수의 집합과 같은 집합이 되고 자연수의 집합과 일대일대응이 되므로 결국 집합 B의 원소의 개수는 집합 A의 개수만큼 많다. 이는 전체가 부분보다 크다는 유클리드 공리에 위배되어 모순이 생긴다.
갈릴레오는 집합 A의 진부분집합인 B의 원소의 개수는 집합 A의 원소의 개수보다 적어야 한다. 그러므로 무한한 원소의 개수를 갖는 두 집합의 크기를 비교할 때는 일대일대응 한다는 것만으로 두 집합의 원소 개수가 같다고 말할 수 없다는 결론을 내린다. 이를 갈릴레이 역설이라고 하는데 이 논리는 게오르크 칸토어의 이론이 나오기 전까지 무려 250년 동안 유지되었다.
집합론의 창시자이자 무한이라는 개념에 많은 연구를 하였던 칸토어는 유클리드 공리인 전체는 부분보다 크다는 것은 유한집합에서 유효하며 무한집합에서는 다르다고 하였다. 칸토어는 무한집합은 진부분집합과 일대일대응이 가능한 집합이라고 정의하였고 갈릴레이의 역설에서 자연수집합의 진부분집합인 제곱수의 집합과 일대일대응이 가능하기에 무한집합이 된다고 하였다. 따라서 제곱수의 집합은 자연수의 집합과 기수가 같다고 하였다. 이러한 개념에서 보면 짝수의 집합, 홀수의 집합 모두 자연수의 집합과 일대일대응이 되므로 기수가 같다.
유리수의 집합은 자연수의 집합과 일대일대응이 될까?
유리수는 b/a (a, b 정수, a는 0이 아니다) 의 형태로 나타내어지므로 순서쌍 (a, b)로 좌표평면에 나타낼 수 있어 규칙성을 갖고 대응시키면 자연수와 일대일대응이 가능하다.
그러나 실수의 집합은 자연수 집합과 일대일대응이 되지 않는다. 자연수와 일대일대응이 되는 무한집합은 셀 수 있어 가산집합(Countable Set)이라고 하고 실수와 같이 자연수와 일대일대응이 되지 않아 셀 수 없는 집합을 비가산집합(Uncountable Set)이라고 한다. 무한집합 중 자연수 집합과 일대일대응이 되는 집합을 가부번집합(denumerable set)이라고 한다.
칸토어는 번뜩이는 아이디어로 실수의 집합은 자연수의 집합과 일대일대응이 되지 않는다는 것을 증명하였다. 실수의 집합과 자연수의 집합은 무한집합이지만 성격이 다른 무한집합인 것이다. 자연수 집합의 기수는 무한집합이므로 무한대가 되지만 무한집합 중 가장 작은 기수를 갖는다고 생각하여 이 값을
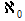
알레프 널 (aleph-null)이라고 하고
실수의 기수는
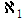
알레프 원(aleph-one)이라고 정의하였다.
'수학 > 중고등학교 수학' 카테고리의 다른 글
| 이항정리의 증명 (2) | 2023.07.21 |
|---|---|
| 심프슨의 역설(simpson’s paradox) (0) | 2023.07.21 |
| 수학으로 본 세 명의 총잡이 결투(게임이론) (1) | 2023.07.13 |
| 확률에서 꼭 알아야 하는 파스칼의 삼각형 (0) | 2023.07.11 |
| 시그마 n번 어떻게 계산할까? (0) | 2023.07.11 |


